170 points, 29 comments
My 4 year old son and I were wondering about soccer ball sized hail today. How much damage would a hail storm with size 5 soccer ball sized hail do?
Michael Grill
When you think about it, it's honestly kind of weird that hailstones haven't killed all of us already. I mean, they're chunks of ice that plunge from the sky!

Hailstones fall from really high up. There's a popular myth that a penny dropped from the Empire State Building can kill you. The myth isn't true,[1] but for anyone who believes it, hailstones should be terrifying—after all, they often fall from the height of ten Empire State Buildings.
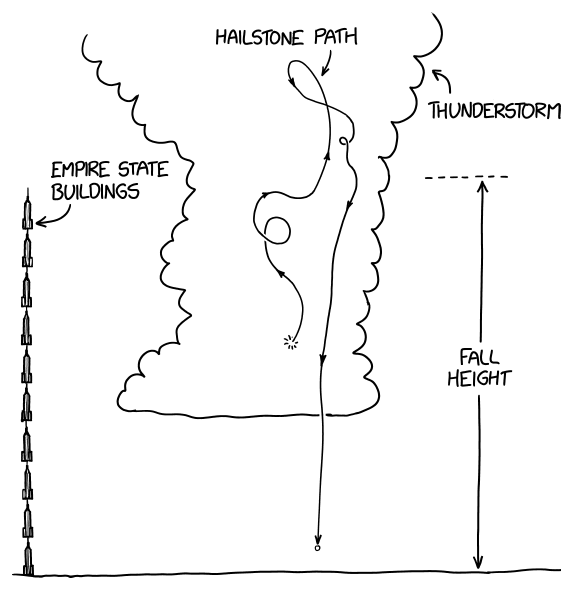
Luckily, the same thing that saves us from falling pennies also generally protects us from hailstones: Air resistance. As they fall, both pennies and hailstones quickly reach terminal velocity, the speed at which drag balances out gravity and prevents them from speeding up any more. For a small hailstone the size of a pea or a marble, terminal velocity might be only 10 or 20 miles per hour, the speed of an object tossed across a room. Getting hit by them isn't comfortable, but it's not likely to cause serious injury.[2]

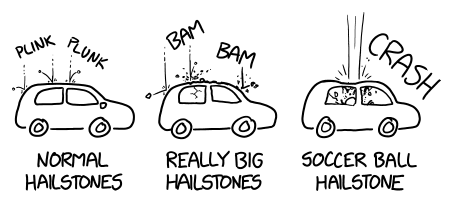
Large hailstones travel much faster than small ones and can be a lot more dangerous. The terminal velocity of a golf-ball-sized hailstone is about 60 miles per hour,[3] which could easily cause serious injury. Large hailstorms often cause extreme damage to cars, and the largest hailstones can be deadly. A storm in China in 2002 dropped egg-sized and baseball-sized hailstones that killed several dozen people and hospitalized many others.
Luckily, deaths from hail aren't very common, for two main reasons: First, because hailstones big enough to be deadly are rare, and second, because when there's a thunderstorm severe enough to produce such large hail, people generally try to take shelter.

A hailstone the size and shape of a regulation soccer ball would be more than twice the weight of the heaviest hailstones on record. It would have a terminal velocity of roughly 140 miles per hour, which is really fast. If one of them hit your car, it wouldn't just dent the body or crack the windshield, it could punch right through the roof. Sheltering indoors might not be enough to protect you, unless you had a particularly sturdy roof or possibly several floors above you.
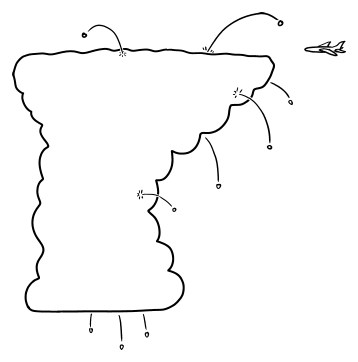
When a hailstorm is nearby, it's good to take shelter even if you're not right below the storm. As a hailstone forms in a thunderstorm updraft, it bounces around like popcorn in a popcorn machine. Usually, it falls out of the bottom of the storm, but sometimes it's ejected out of the top or sides, then carried by wind to fall some distance from the storm. Aircraft flying near thunderstorms have been hit by hail when they have nothing but blue sky above them.
Real hailstones, especially large ones, aren't round like a soccer ball. As they tumble around in a thunderstorm, they grow via water freezing onto their sides. If they have a lump on one side, the protrusion can collect more water and grow faster than the areas around it, forming a blobby appendage. Liquid water can also run out to the edges of a rotating hailstone and freeze, forming icicle-like features.
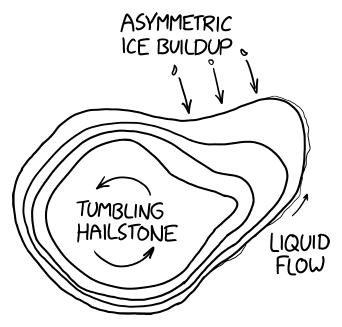
The weird shapes of large hailstones are good news for us ground-dwellers with breakable bones, because these protrusions tend to increase their drag and lower their terminal velocity.
But the weird shapes of hailstones also raises an interesting possibility. If a hailstone had just the right combination of lobes, it's possible—if unlikely—that it might happen to form a lifting body. This strange category of aircraft—which includes the Space Shuttle, the M2-F1, and the Dream Chaser—can be unexpectedly aerodynamic despite their compact shapes, capable of gliding or even swoops.
It's unlikely that any gliding hail has ever been observed, but in the 4 billion years that Earth has had water and thunderstorms, there have probably been some pretty strange hailstones. Not only has there likely been one the size of a soccer ball ...
... there might even have been one able to score a goal.
[1] Mythbusters tried it in Season 1 Episode 7 and found that the penny would really sting and make you go "ow!!"
[2] While dropping a penny on someone from the height of the Empire State Building wouldn't kill them, dropping the Empire State Building on a them from the height of a penny would, as demonstrated by the tragic demise of Jebediah Mythbuster in the pilot episode of the show eventually named in his memory.
[3] A little slower than an actual golf ball, thanks to the golf ball's greater weight and those weird drag-reducing dimples.